Moved to new blog
In a previous article, I described the basics of binary arithmetic and gave a function to display the binary representation of a number. Here, we’ll look at several ways to count the set (1) bits in a number.
First of all, why would you want to count bits? Bitsets. If you use bitsets as a fast set implementation, you might want to find out how many elements there are in the set. I used this in a sudoku programme to memorise which digits can’t be placed in a particular cell. Bit counting functions are also used extensively in graphics (bitmap manipulations).
Here’s 22 in binary:00010110
From the binary representation, it’s obvious that there are 3 set bits and 5 unset bits. How do you count them? I’ll give three methods.
Classic, let’s iterate through every bit, solution
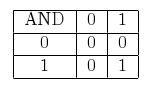
The idea behind this is simple: take every bit in the number (n) and check if it’s 1. To do this, you can simply use a variable (i):
- initialise i with 1
- check if n AND i is greater than zero and if so, increment a counter
- multiply i by 2
- if i < n, go to 2
Here’s the code:
/* Count the ON bits in n using an iterative algorithm */
int bitcount(int n) {
int tot = 0;
int i;
for (i = 1; i <= n; i = i<<1)
if (n & i)
++tot;
return tot;
}
This isn’t bad and works in O(lg(n)) time, but if you know (you probably will) if the number is made up mostly of ones or zeros, use one of the following algorithms.
Sparse ones algorithm
This solution relies on the following observation:2210 = 000101102
22 - 1 = 2110 = 000101012
22 AND 21 = 00010100
Notice what happened: by logically ANDing 22 and 21, you get a number whose binary representation is the same as 22 but with the last 1 flipped to 0.
The idea behind this algorithm is to logically AND n and n – 1 until n is 0. The number of times necessary to do this will the the number of 1 bits.
Here’s the code:
/* Counts the ON bits in n. Use this if you know n is mostly 0s */
int bitcount_sparse_ones(int n) {
int tot = 0;
while (n) {
++tot;
n &= n - 1;
}
return tot;
}
Why call it sparse ones? Look at the algorithm, and apply it to a few numbers on a piece of paper. You’ll notice that you go through the inner loop the x times, where x is the number of 1s in the number. So the time is O(x), and it’s best to use it if there are few ones in the number.
Dense ones algorithm
But what if your number is mostly 1? The solution is obvious: flip every bit in n, then apply the sparse ones algorithm:
/* Counts the ON bits in n. Use this if you know n is mostly 1s */
int bitcount_dense_ones(int n) {
int tot = 0;
n ^= (unsigned int)-1;
while (n) {
++tot;
n &= n - 1;
}
return sizeof(int) * 8 - tot;
}
Full source
Here’s the full C source to the programme (bit.c):
NOTE: Source is mangled by WordPress. Don’t copy-paste; download the file.
#include <stdio.h>
/* Print n as a binary number */
void printbits(int n) {
unsigned int i, step;
if (0 == n) { /* For simplicity's sake, I treat 0 as a special case*/
printf("0000");
return;
}
i = 1<<(sizeof(n) * 8 - 1);
step = -1; /* Only print the relevant digits */
step >>= 4; /* In groups of 4 */
while (step >= n) {
i >>= 4;
step >>= 4;
}
/* At this point, i is the smallest power of two larger or equal to n */
while (i > 0) {
if (n & i)
printf("1");
else
printf("0");
i >>= 1;
}
}
/* Count the ON bits in n using an iterative algorithm */
int bitcount(int n) {
int tot = 0;
int i;
for (i = 1; i <= n; i = i<<1)
if (n & i)
++tot;
return tot;
}
/* Counts the ON bits in n. Use this if you know n is mostly 0s */
int bitcount_sparse_ones(int n) {
int tot = 0;
while (n) {
++tot;
n &= n - 1;
}
return tot;
}
/* Counts the ON bits in n. Use this if you know n is mostly 1s */
int bitcount_dense_ones(int n) {
int tot = 0;
n ^= (unsigned int)-1;
while (n) {
++tot;
n &= n - 1;
}
return sizeof(int) * 8 - tot;
}
int main(int argc, char *argv[]) {
int i;
for (i = 0; i < 23; ++i) {
printf("%d = ", i);
printbits(i);
printf("\tON bits: %d %d %d", bitcount(i), bitcount_sparse_ones(i), bitcount_dense_ones(i));
printf("\n");
}
return 0;
}
That’s it. If you’re intrested in a few more (slightly esoteric) algorithms, see this article.
Good luck. Always open to comments.