Computer programming

Sudoku is that Japanese puzzle that requires you to fill in a grid of numbers. Here, I describe a general algorithm to solve these puzzles. Also provided is the source code in C++.

You can see a Sudoku board below. The goal is to fill in every empty cell with a number between 1 and 9 so that no number repeats itself on any line, column of zone (three-by-three marked square).

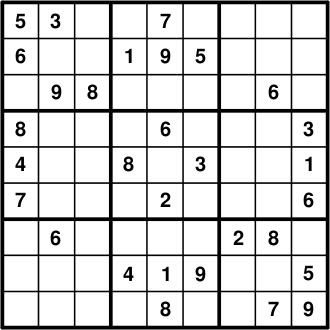
If you’ve never solved a Sudoku before, now would be the time to do it. Wikipedia describes some useful strategies.

How do you approach a problem like this? The simplest way is from input to output. What’s your input? It’s a 9×9 matrix of numbers like this one:

5 3 0   0 7 0   0 0 0
6 0 0   1 9 5   0 0 0
0 9 8   0 0 0   0 6 0
8 0 0   0 6 0   0 0 3
4 0 0   8 0 3   0 0 1
7 0 0   0 2 0   0 0 6
0 6 0   0 0 0   2 8 0
0 0 0   4 1 9   0 0 5
0 0 0   0 8 0   0 7 9

How do you store it in the programme? If you said as a matrix, you were close. A matrix is obvious, it’s easy to understand, but it’s a pain to code. Believe me when I say, it’s a lot easier to store it as an array of 9*9 elements. What else do you need? A variable to keep track of how many cells have been filled in (0 means empty board; 81 means full board). An array of bitsets to keep track of what digits can’t be used in each cell (I’ll explain a little later), and the setter and getter functions. As it happens, it’s also easier if you encapsulate it in a C++ class. Here’s the full code to the programme (sudoku.cpp). I’ll explain it all in a bit.

#include <iostream>
#include <fstream>

using namespace std;

class SudokuBoard;
void printB(SudokuBoard sb);

typedef unsigned int uint;

const uint MAXVAL = 9;
const uint L = 9;
const uint C = 9;
const uint S = L * C;
const uint ZONEL = 3;
const uint ZONEC = 3;
const uint ZONES = ZONEL * ZONEC;

const uint lineElements[L][C] = {
	{ 0,  1,  2,  3,  4,  5,  6,  7,  8},
	{ 9, 10, 11, 12, 13, 14, 15, 16, 17},
	{18, 19, 20, 21, 22, 23, 24, 25, 26},
	{27, 28, 29, 30, 31, 32, 33, 34, 35},
	{36, 37, 38, 39, 40, 41, 42, 43, 44},
	{45, 46, 47, 48, 49, 50, 51, 52, 53},
	{54, 55, 56, 57, 58, 59, 60, 61, 62},
	{63, 64, 65, 66, 67, 68, 68, 70, 71},
	{72, 73, 74, 75, 76, 77, 78, 79, 80}
};

const uint columnElements[C][L] = {
	{ 0,  9, 18, 27, 36, 45, 54, 63, 72},
	{ 1, 10, 19, 28, 37, 46, 55, 64, 73},
	{ 2, 11, 20, 29, 38, 47, 56, 65, 74},
	{ 3, 12, 21, 30, 39, 48, 57, 66, 75},
	{ 4, 13, 22, 31, 40, 49, 58, 67, 76},
	{ 5, 14, 23, 32, 41, 50, 59, 68, 77},
	{ 6, 15, 24, 33, 42, 51, 60, 69, 78},
	{ 7, 16, 25, 34, 43, 52, 61, 70, 79},
	{ 8, 17, 26, 35, 44, 53, 62, 71, 80}
};

const uint zoneElements[S / ZONES][ZONES] = {
	{ 0,  1,  2,  9, 10, 11, 18, 19, 20},
	{ 3,  4,  5, 12, 13, 14, 21, 22, 23},
	{ 6,  7,  8, 15, 16, 17, 24, 25, 26},
	{27, 28, 29, 36, 37, 38, 45, 46, 47},
	{30, 31, 32, 39, 40, 41, 48, 49, 50},
	{33, 34, 35, 42, 43, 44, 51, 52, 53},
	{54, 55, 56, 63, 64, 65, 72, 73, 74},
	{57, 58, 59, 66, 67, 68, 75, 76, 77},
	{60, 61, 62, 68, 70, 71, 78, 79, 80}
};

class SudokuBoard {
public:
	SudokuBoard() :
		filledIn(0)
	{
		for (uint i(0); i < S; ++i)
			table[i] = usedDigits[i] = 0;
	}

	virtual ~SudokuBoard() {
	}

	int const at(uint l, uint c) { // Returns the value at line l and row c
		if (isValidPos(l, c))
			return table[l * L + c];
		else
			return -1;
	}

	void set(uint l, uint c, uint val) { // Sets the cell at line l and row c to hold the value val
		if (isValidPos(l, c) && ((0 < val) && (val <= MAXVAL))) {
			if (table[l * C + c] == 0)
				++filledIn;
			table[l * C + c] = val;
			for (uint i = 0; i < C; ++i) // Update lines
				usedDigits[lineElements[l][i]] |= 1<<val;
			for (uint i = 0; i < L; ++i) // Update columns
				usedDigits[columnElements[c][i]] |= 1<<val;
			int z = findZone(l * C + c);
			for (uint i = 0; i < ZONES; ++i) // Update columns
				usedDigits[zoneElements[z][i]] |= 1<<val;
		}
	}

	void solve() {
		try { // This is just a speed boost
			scanAndSet(); // Logic approach
			goBruteForce(); // Brute force approach
		} catch (int e) { // This is just a speed boost
		}
	}

	void scanAndSet() {
		int b;
		bool changed(true);
		while (changed) {
			changed = false;
			for (uint i(0); i < S; ++i)
				if (0 == table[i]) // Is there a digit already written?
					if ((b = bitcount(usedDigits[i])) == MAXVAL - 1) { // If there's only one digit I can place in this cell, do
						int d(1); // Find the digit
						while ((usedDigits[i] & 1<<d) > 0)
							++d;
						set(i / C, i % C, d); // Fill it in
						changed = true; // The board has been changed so this step must be rerun
					} else if (bitcount(usedDigits[i]) == MAXVAL)
						throw 666; // Speed boost
		}
	}

	void goBruteForce() {
		int max(-1); // Find the cell with the _minimum_ number of posibilities (i.e. the one with the largest number of /used/ digits)
		for (uint i(0); i < S; ++i)
			if (table[i] == 0) // Is there a digit already written?
				if ((max == -1) || (bitcount(usedDigits[i]) > bitcount(usedDigits[max])))
					max = i;

		if (max != -1) {
			for (uint i(1); i <= MAXVAL; ++i) // Go through each possible digit
				if ((usedDigits[max] & 1<<i) == 0) { // If it can be placed in this cell, do
					SudokuBoard temp(*this); // Create a new board
					temp.set(max / C, max % C, i); // Complete the attempt
					temp.solve(); // Solve it
					if (temp.getFilledIn() == S) { // If the board was completely solved (i.e. the number of filled in cells is S)
						for (uint j(0); j < S; ++j) // Copy the board into this one
							set(j / C, j % C, temp.at(j / C, j % C));
						return; // Break the recursive cascade
					}
				}
		}
	}

	uint getFilledIn() {
		return filledIn;
	}

private:
	uint table[S];
	uint usedDigits[S];
	uint filledIn;

	bool const inline isValidPos(int l, int c) {
		return ((0 <= l) && (l < (int)L) && (0 <= c) && (c < (int)C));
	}

	uint const inline findZone(uint off) {
		return ((off / C / ZONEL) * (C / ZONEC) + (off % C / ZONEC));
	}

	uint const inline bitcount(uint x) {
		uint count(0);
		for (; x; ++count, x &= (x - 1));
		return count;
	}
};

void printB(SudokuBoard sb) {
	cout << "  |  -------------------------------  |" << endl;
	for (uint i(0); i < S; ++i) {
		if (i % 3 == 0)
			cout << "  |";
		cout << "  " << sb.at(i / L, i % L);
		if (i % C == C - 1) {
			if (i / C % 3 == 2)
				cout << "  |" << endl << "  |  -------------------------------";
			cout << "  |" << endl;
		}
	}
	cout << endl;
}

int main(int argc, char *argv[]) {
	SudokuBoard sb;

	ifstream fin("sudoku4.in");
	int aux;
	for (uint i(0); i < S; ++i) {
		fin >> aux;
		sb.set(i / L, i % L, aux);
	}
	fin.close();

	printB(sb);
	sb.solve();
	printB(sb);

	return 0;
}

Look at the main function. It first opens a file and then reads S ints from it. S is just the number of columns (C) multiplied by the number of lines (L). It reads the value into an auxiliary variable and then sets it in the SudokuBoard.

How does it set a cell? The relevant code is in set. The first line just checks if the parameters are valid (if the value’s not too large, if the specified cell does not exist, etc.). Then it checks if there’s a value already in the cell (there shouldn’t be). If not, it increments the number of filled-in cells.

Now things get intresting. If a certain cell contains the number n, it should be obvious that none of the cells on the same line, column or zone as the cell can contain n. Look at the board above: because there’s a 5 in cell 1,1, there can’t be any more fives in any of the cells on the first line, on the first column or in the upper-left zone. This is what the remainder of set does. It sets the n^th bit in every bitset in whose corresponding cell the number n cannot appear.

Note: For a given cell, it’s trivial to find the line, column and zone in which it happens to be. What’s hard is to find the other cells in the same line, column or zone. To keep things simple, use three arrays of arrays that contain the number of the cells on a certain line, column or zone.

The next function of intrest is solve. If you’ll look at it, you’ll notice that it contains a try…except statement. As the comments clearly note, it’s just a speed boost. If you comment it out, the programme will still work (but in some cases a lot slower).

Solve calls two other functions: scanAndSet and goBruteForce. These are both algorithms to determine or guess what value should be placed in which cell.

scanAndSet

void scanAndSet() {
	int b;
	bool changed(true);
	while (changed) {
		changed = false;
		for (uint i(0); i < S; ++i)
			if (0 == table[i]) // Is there a digit already written?
				if ((b = bitcount(usedDigits[i])) == MAXVAL - 1) { // If there's only one digit I can place in this cell, do
					int d(1); // Find the digit
					while ((usedDigits[i] & 1<<d) > 0)
						++d;
					set(i / C, i % C, d); // Fill it in
					changed = true; // The board has been changed so this step must be rerun
				} else if (bitcount(usedDigits[i]) == MAXVAL)
					throw 666; // Speed boost
	}
}

The basic idea is this: we have a list of cells that need to be completed (those whose value is 0) and list of digits that cannot be placed in each cell. Go through the list of used digits, searching for a cell in which 8 digits cannot be placed (i.e. there’s only one digit that can be placed), and place it.

Now, every time you place a digit, you change the board a bit, restricting the digits that can be placed in other cells. So, you have to do the previous step until you don’t change anything any more.

There’s also a check in there if the number of used digits for any cell is 9 (i.e. no digit can be placed in the cell). If such a cell exists then the board is clearly wrong, so throw an exception (which is caught in the solve routine).

goBruteForce

void goBruteForce() {
	int max(-1); // Find the cell with the _minimum_ number of posibilities (i.e. the one with the largest number of /used/ digits)
	for (uint i(0); i < S; ++i)
		if (table[i] == 0) // Is there a digit already written?
			if ((max == -1) || (bitcount(usedDigits[i]) > bitcount(usedDigits[max])))
				max = i;

	if (max != -1) {
		for (uint i(1); i <= MAXVAL; ++i) // Go through each possible digit
			if ((usedDigits[max] & 1<<i) == 0) { // If it can be placed in this cell, do
				SudokuBoard temp(*this); // Create a new board
				temp.set(max / C, max % C, i); // Complete the attempt
				temp.solve(); // Solve it
				if (temp.getFilledIn() == S) { // If the board was completely solved (i.e. the number of filled in cells is S)
					for (uint j(0); j < S; ++j) // Copy the board into this one
						set(j / C, j % C, temp.at(j / C, j % C));
					return; // Break the recursive cascade
				}
			}
	}
}

If you comment the call to this procedure in solve you’ll notice that there are some boards that are not completed by scanAndSet. Why? Because there are some boards that can’t be completed through logic alone (and ours isn’t particularly thorough either).

To get over this, you have to use a brute-force algorithm. The idea is simple enough: given the list of which digits cannot be placed in each cell, find the cell in which the minimum number of digits can be placed. For this cell, for every possible digit, write it down and try to solve the board.

This is where it becomes apparent why a C++ object-oriented approach is a smart move. Instead of writing the try in the current board and then having to keep track of what changes are made, simply clone the current board, fill in a cell and let it solve itself.

That’s it. You might want to try some of the other algorithms suggested on the Net. Good luck. Always open to comments.

In this article I’ll begin by defining binary numbers and describe the basic operations. Afterwords, I’ll show you several of the most common uses of binary numbers.

Humans work with digits in base 10, and we’re quite good at it. Computers, on the other hand, use base 2 and it shouldn’t come as a surprise that they’re extremely good at it. Today’s high level languages do a lot to hide this fact from us, but, still, a fairly good grasp of binary numbers is essential to working with computers, especially programming them.

Binary numbers

Mathworld defines binary as:

The base 2 method of counting in which only the digits 0 and 1 are used.

Basically, the binary representation of a number is the way of writing that number, uniquely, using only the digits 0 and 1. These are the binary representations of the first 16 natural numbers:

0 = 0000
1 = 0001
2 = 0010
3 = 0011
4 = 0100
5 = 0101
6 = 0110
7 = 0111
8 = 1000
9 = 1001
10 = 1010
11 = 1011
12 = 1100
13 = 1101
14 = 1110
15 = 1111

Given a number in base 10, how do you find the representation in base 2? You take the number and divide it repeatedly by 2 taking note of the remainder. After you’ve reached 0, write the remainders in reverse order. That’s the binary number! Here’s an example for 13:

So,

Now, how do you get a decimal form a binary? This is even easier. Take the number in binary form and start from the right side. Multiply the first digit (from the right side) with 2⁰. Multiply the second digit with 2¹ and add it to the result from the first multiplication. Multiply the third digit with 2² and add it to what you have so far. … Do this for all the digits and you’ll get the decimal representation of the binary number.

Logical operations

All of the following operations work in the same way. Take every bit form the first number and the corresponding bit from the second number (if it exists) and compute the resulting bit using the operation’s truth table.

NOT

So, take each bit and reverse it.

0000 becomes 1111
0101 becomes 1010
1111 becomes 0000

It’s worthwhile to note that applying NOT twice, you get the original number unaltered.

AND

So, if both digits are 1 then the result is 1, otherwise it is 0.

OR

So, if either digit is 1, then the result is 1, otherwise it is 0.

XOR (eXclusive OR)

So, if one of the digits it 1, but not both, then the result is 1, otherwise, the result is 0.

SHL (SHift Left) and SHR (SHift Right)

These aren’t like the other operations in that they don’t rely on truth tables. To apply them, simply drop the left-most (right-most) digit and add a 0 digit to the right (left).

After successive SHL operations,

0011 becomes 0110,
0110 becomes 1100,
1100 becomes 1000,
1000 becomes 0000

After successive SHR operations,

1100 becomes 0110,
0110 becomes 0011,
0011 becomes 0001,
0001 becomes 0000

Common use: Fast multiplication/division by 2

To quickly multiply an integer by 2, simply shift left the number.

To quickly divide an integer by 2, simply shift right the number.

In C, this would be:

a = a <> 1; /* Divide by 2 */
a = a >> 1; /* Multiply by 2*/

Setting/Checking a certain bit

To check whether the (n + 1)^th bit is set (1) or not (0), use this:

a & 1<<n = 0 if the bit is NOT set
a & 1< 0 if the bit is set

To set the (n + 1)^th bit, use this:

a = a | 1<<n;

What am I doing here? In both cases I first compute 1<<n. This is a binary number in which all digits are 0 but the n^th digit is 1. Then, to check, I logically AND the two numbers. If the bit is set, then the result should be anything but 0. On the other hand, to set the bit, I logically OR the two numbers. If the bit was set, than this will have no effect. But if the bit was not set, it will be at the end.

Common use: bitsets

Chances are, at one time or another, you’ve had to use an array of boolean values. You’ve probably used something like this:

char foo[100];
foo[42] = 0; /* Equivalent of false */
foo[42] = 1; /* Equivalent of true*/

OR

bool bar[100];
bar[23] = false;
bar[23] = true;

This isn’t bad. Actually, in most cases it’s quite good. But if the number of elements is relatively small (less than 64), there’s a better way, that is using bitsets.

Instead of an array use an int, then use the methods described above to set and check the bits.

int a;
a = 0; /* The entire ``array" is set to false */
a |= 1<<3; /* The fourth bit is set */
if (a & 1<<3) /* Is the fourth bit set? */
        a ^= 1<<3; /* If it is, flip it. */

Flipping bits

To flip a bit, XOR it by 1.

a ^= 1<<5; /* Flip the sixth bit */

Putting it all together: Printing a binary number

This small C programme prints out the binary representation of 0, 1, …, 16. (bit.c)

#include <stdio.h>

/* Print n as a binary number */
void printbitssimple(int n) {
	unsigned int i;
	i = 1<<(sizeof(n) * 8 - 1);

	while (i > 0) {
		if (n & i)
			printf("1");
		else
			printf("0");
		i >>= 1;
	}
}

/* Print n as a binary number */
void printbits(int n) {
	unsigned int i, step;

	if (0 == n) { /* For simplicity's sake, I treat 0 as a special case*/
		printf("0000");
		return;
	}

	i = 1<<(sizeof(n) * 8 - 1);

	step = -1; /* Only print the relevant digits */
	step >>= 4; /* In groups of 4 */
	while (step >= n) {
		i >>= 4;
		step >>= 4;
	}

	/* At this point, i is the smallest power of two larger or equal to n */
	while (i > 0) {
		if (n & i)
			printf("1");
		else
			printf("0");
		i >>= 1;
	}
}

int main(int argc, char *argv[]) {
	int i;
	for (i = 0; i < 16; ++i) {
		printf("%d = ", i);
		printbits(i);
		printf("\n");
	}

	return 0;
}

Code should be fairly easy to understand. Good luck. Always open to comments. Update: The next article in this series is Counting Bits.