Moved to new blog
In this article, I describe the Bellman-Ford algorithm for finding the one-source shortest paths in a graph, give an informal proof and provide the source code in C for a simple implementation.
To understand this you should know what a graph is, and how to store one in memory. If in doubt check this and this.
Another solution to this problem is Dijkstra’s algorithm.
The Problem
Given the following graph, calculate the length of the shortest path from node 1 to node 2.
It’s obvious that there’s a direct route of length 6, but take a look at path: 1 -> 4 -> 3 -> 2. The length of the path is 7 – 3 – 2 = 2, which is less than 6. BTW, you don’t need negative edge weights to get such a situation, but they do clarify the problem.
This also suggests a property of shortest path algorithms: to find the shortest path form x to y, you need to know, beforehand, the shortest paths to y‘s neighbours. For this, you need to know the paths to y‘s neighbours’ neighbours… In the end, you must calculate the shortest path to the connected component of the graph in which x and y are found.
That said, you usually calculate the shortest path to all nodes and then pick the ones you’re intrested in.
The Algorithm
The Bellman-Ford algorithm is one of the classic solutions to this problem. It calculates the shortest path to all nodes in the graph from a single source.
The basic idea is simple:
Start by considering that the shortest path to all nodes, less the source, is infinity. Mark the length of the path to the source as 0:
Take every edge and try to relax it:
Relaxing an edge means checking to see if the path to the node the edge is pointing to can’t be shortened, and if so, doing it. In the above graph, by checking the edge 1 -> 2 of length 6, you find that the length of the shortest path to node 1 plus the length of the edge 1 -> 2 is less then infinity. So, you replace infinity in node 2 with 6. The same can be said for edge 1 -> 4 of length 7. It’s also worth noting that, practically, you can’t relax the edges whose start has the shortest path of length infinity to it.
Now, you apply the previous step n – 1 times, where n is the number of nodes in the graph. In this example, you have to apply it 4 times (that’s 3 more times).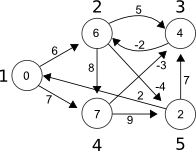


That’s it, here’s the algorithm in a condensed form:
void bellman_ford(int s) {
int i, j;
for (i = 0; i < n; ++i)
d[i] = INFINITY;
d[s] = 0;
for (i = 0; i < n - 1; ++i)
for (j = 0; j < e; ++j)
if (d[edges[j].u] + edges[j].w < d[edges[j].v])
d[edges[j].v] = d[edges[j].u] + edges[j].w;
}
Here, d[i] is the shortest path to node i, e is the number of edges and edges[i] is the i-th edge.
It may not be obvious why this works, but take a look at what is certain after each step. After the first step, any path made up of at most 2 nodes will be optimal. After the step 2, any path made up of at most 3 nodes will be optimal… After the (n – 1)-th step, any path made up of at most n nodes will be optimal.
The Programme
The following programme just puts the bellman_ford function into context. It runs in O(VE) time, so for the example graph it will do something on the lines of 5 * 9 = 45 relaxations. Keep in mind that this algorithm works quite well on graphs with few edges, but is very slow for dense graphs (graphs with almost n2 edges). For graphs with lots of edges, you’re better off with Dijkstra’s algorithm.
Here’s the source code in C (bellmanford.c):
#include <stdio.h>
typedef struct {
int u, v, w;
} Edge;
int n; /* the number of nodes */
int e; /* the number of edges */
Edge edges[1024]; /* large enough for n <= 2^5=32 */
int d[32]; /* d[i] is the minimum distance from node s to node i */
#define INFINITY 10000
void printDist() {
int i;
printf("Distances:\n");
for (i = 0; i < n; ++i)
printf("to %d\t", i + 1);
printf("\n");
for (i = 0; i < n; ++i)
printf("%d\t", d[i]);
printf("\n\n");
}
void bellman_ford(int s) {
int i, j;
for (i = 0; i < n; ++i)
d[i] = INFINITY;
d[s] = 0;
for (i = 0; i < n - 1; ++i)
for (j = 0; j < e; ++j)
if (d[edges[j].u] + edges[j].w < d[edges[j].v])
d[edges[j].v] = d[edges[j].u] + edges[j].w;
}
int main(int argc, char *argv[]) {
int i, j;
int w;
FILE *fin = fopen("dist.txt", "r");
fscanf(fin, "%d", &n);
e = 0;
for (i = 0; i < n; ++i)
for (j = 0; j < n; ++j) {
fscanf(fin, "%d", &w);
if (w != 0) {
edges[e].u = i;
edges[e].v = j;
edges[e].w = w;
++e;
}
}
fclose(fin);
/* printDist(); */
bellman_ford(0);
printDist();
return 0;
}
And here’s the input file used in the example (dist.txt):
5
0 6 0 7 0
0 0 5 8 -4
0 -2 0 0 0
0 0 -3 9 0
2 0 7 0 0That’s an adjacency matrix.
That’s it. Have fun. Always open to comments.